闲扯
define ll真好用
一道比较基础的线段树题,只是前期推式子要注意。
题面
Solution
我们可以先将每条连接 $u,v(u<v)$ 公路都对应到 $u$ 上。
因为是等概率选择,所以我们只需要求出所有情况下费用的和,再除以情况数即可。
考虑怎么计算费用。
这里有两种想法:
- 统计每一条被计算了几次。
- 直接计算所有的情况。
根据本人的测试,第一种要好写的多。第二种是维护前缀和,但是有区间加的操作,貌似不好维护或者根本没法维护。
推式子。
因为对于每一条公路,我们都将它对应到了编号较小的点上,所以我们实际需要统计的只有 $l\sim r-1$ 这一段的答案。
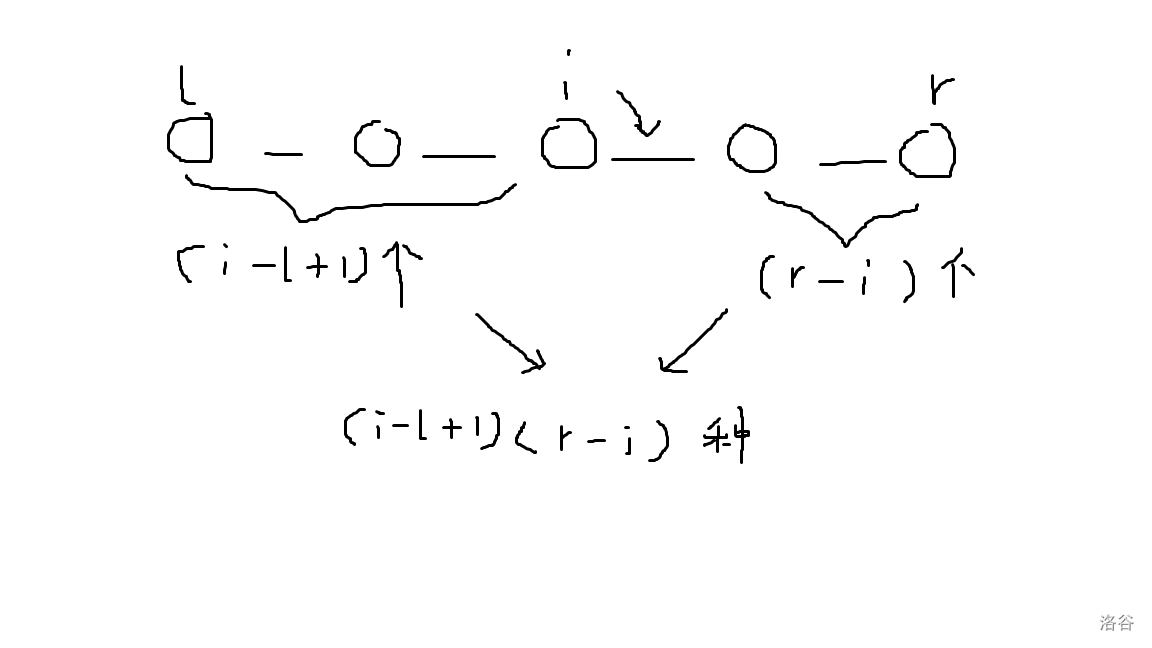
所以我们只需要维护 $\sum w_i,\sum w_i\cdot i,\sum w_i\cdot i^2$ 这三个变量即可。
对于第一个,我们直接维护就好。
对于第二个,我们可以得出增加量为 $\frac{r\cdot(r+1)}{2}\cdot v-\frac{l\cdot(l-1)}{2}\cdot v$ 。
对于第三个,我们可以得出增加量为 $\frac{r\cdot(r+1)\cdot(2\cdot r+1)}{6}\cdot v-\frac{(l-1)\cdot l\cdot(2\cdot l-1)}{6}\cdot v$ 。
然后上线段树就行。
Code
1 |
|
总结
在做乘法的时候一定要注意会不会爆 $int$ 。